Sketch and evaluate the integral region $x \ge 0, x^2+y^2 \le 2, x^2+y^2\ge 1$

enter image description here" />

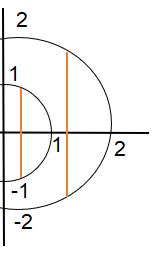
Sketch the region defined by $x \ge 0, x^2+y^2 \le 2, x^2+y^2\ge 1$ . Write down the integral over the region in each of the two possible orders of $f(x,y) = x^2$ . Evaluate both integrals. In defining the regions of integration, I imagine it to look something like this: By taking the integral verticallyt in respect to $y$ I then get: $x \le\sqrt$ , so $y$ has the bounds $-\sqrtshould do with $x$ and $y$ , any ideas will be appreciated!

• multivariable-calculus
• multiple-integral

$\begingroup$ shouldn't you have $\sqrt 2$ because $x^2+y^2=r^2$ so, $x^2+y^2\leq 2$ and thus $r\leq\sqrt 2$ $\endgroup$

2 Answers 2

If you want to integrate first in order to $y$ and then in order to $x$ , then start by noting that $0\leqslant x\leqslant\sqrt2$ (see the picture below). If $0\leqslant x\leqslant1$ , then $y$ takes values from $-\sqrt$ to $-\sqrt$ and from $\sqrt$ to $\sqrt$ , whereas if $1\leqslant x\leqslant\sqrt2$ , then $y$ takes values from $-\sqrt$ to $\sqrt$ . So, you have $$\int_0^1\left(\int_<-\sqrt>^<-\sqrt>x^2\,\mathrm dy+\int_<\sqrt>^<\sqrt>x^2\,\mathrm dy\right)\,\mathrm dx+\int_1^\int_<-\sqrt>^<\sqrt>x^2\,\mathrm dy\,\mathrm dx.$$

And if you integrate first in order to $x$ and then in order to $y$ , by a similar reason you should get $$\int_^\int_0^>x^2\,\mathrm dx\,\mathrm dy+\int_^1\int_>^>x^2\,\mathrm dx\,\mathrm dy+\int_1^\int_0^>x^2\,\mathrm dx\,\mathrm dy.$$

enter image description here" />

$\begingroup$ This does help! Though I do not understand why there are three separate integral equations taking place? Could you provide some detail on this please, I'm in deep appreciation of your support Jose! $\endgroup$

$\begingroup$ Aha! I think I may have figured it out. We are integrating in respect to y when $0\le x\le1$ and at this point as given in the image, it takes both the positive and negative values of the region. Whereas for $0\le x \le \sqrt<2>$, y only takes the values from the circle $x^2+y^2 \le 2$. I had second guessed myself on this approach as I haven't tried it before, so this really helps cement my ideas! $\endgroup$

Note
In this note, the constant of integration will be ignored.

Let $I = \int \sin^2(u) ~du.$

Then, $~\cos(2u) = 1 - 2\sin^2(u)~$ which implies $~\int [1 - \cos(2u)] du = 2I.$

Therefore $~~~\displaystyle u - \frac\sin(2u) = 2I.$

Therefore $$\fracu - \frac\sin(2u) = I.\tag1$$

Note
In both of the integrals below, trig substitutions will be employed where the pertinent angle $\theta$ (et al) is restricted to $0 \leq \theta \leq \pi/2$ . Under this restriction, both $\cos(\theta)$ and $\sin(\theta)$ will be non-negative throughout the interval.

For the smaller circle: $y = \sqrt$

So, you have $\int_0^1 2\sqrt ~dx.$

Because of the nature of the integral, integration by trig substitution suggests itself.

Let $\cos(u) = x \implies \sqrt = \sin(u)$ .
Then $-\sin(u)du = dx.$
Further, as $x$ goes from $(0)$ to $(1)$ , $u$ goes from $(\pi/2)$ to $(0).$

Therefore, the first integral becomes

Using (1) above, (2) is evaluated as

Since $\sin(2 \times 0) = 0 = \sin(2 \times \pi/2)$ , (2) evaluates to $(\pi/2).$

For the larger circle: $y = \sqrt$

The trig substitution here is a little trickier.

Let $\sqrt\cos(u) = x \implies \sqrt = \sqrt\sin(u)$ .
Then $-\sqrt\sin(u)du = dx.$
Further, as $x$ goes from $(0)$ to $(\sqrt)$ , $u$ goes from $(\pi/2)$ to $(0).$

Therefore, the second integral becomes

Using (1) above, (3) is evaluated as

Again, since $\sin(2 \times 0) = 0 = \sin(2 \times \pi/2)$ , (3) evaluates to $(\pi).$

Addendum
For what it's worth, the inspiration behind the trig substitutions was the assumption that you have a 1st quadrant circular arc [centered at $(0,0)$ ] of radius $r$ . Here, as $u$ goes from $(0)$ to $(\pi/2)$ , $(x,y)$ may be represented by $[r\cos(u), r\sin(u)].$